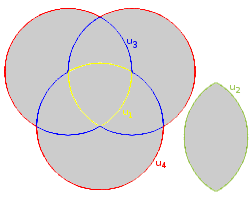
Berechnungen mit drei gleichgroßen Kreisen, welche sich so schneiden, dass der Mittelpunkt jedes Kreises auf einem Schnittpunkt der beiden anderen liegt. Der Abstand der Mittelpunkte zweier Kreise entspricht dem Radius. Die Schnittmenge aller drei Kreise mit der Fläche A1 ist das Reuleaux-Dreieck. Geben Sie einen Wert ein (r, u1, u2, u3, u4, A1 oder A2), runden Sie bei Bedarf und klicken Sie auf Berechnen.
Radien und Umfang haben die gleiche Einheit (beispielsweise Meter), der Flächeninhalt hat diese Einheit zum Quadrat (beispielsweise Quadratmeter).
Die innerste Form mit der Fläche A1 und dem Umfang u1 ist das Reuleaux-Dreieck, für welches es Anwendungen in der Mechanik gibt. Die Form A2 wird hier als spitzes Oval bezeichnet und ist eine Zusammensetzung aus zwei gleichen Kreissegmenten. Die Form A3 ist der Umriss einer Triqueta, manchmal auch Dreischenkel genannt. Die Triqueta wird mit den inneren Kreisbögen gezeichnet, wie der blaue und gelbe Bereich in der Skizze der Umfänge u1 und u3. Sie ist unter anderem von uramerikanischen Kulturen, sowie von den Kelten und Germanen bekannt. Als Dreipass bezeichnet man die nach außen weisenden Kreisbögen der drei gleichen, regelmäßigen Kreise A4. Dreipasse wurden in den europäischen Kulturen ab der Spätromanik und durch die ganze Gotik hindurch als Zierelemente genutzt und finden sich noch häufig in Kirchenbauten aus jener Zeit. Es werden allerdings noch andere Formen, welche auf drei gleichen Teilen basieren, als Dreipass bezeichnet.
Die drei auf diese Weise angeordneten Kreise erzeugen also mehrere Formen, welche für verschiedene Kulturen unterschiedlichste Rollen spielten und spielen. Eine Form, welche auch darinnen steckt, aber anscheinend wenig Verwendung findet ist die der Schnittmenge zweier Kreise minus die Schnittmenge der drei Kreise. Ihr Flächeninhalt ist A2-A1, ihr Umfang u1.
