Heptagon Calculator

Name: Regular Heptagon - Geometry Calculator
Author: Jürgen Kummer

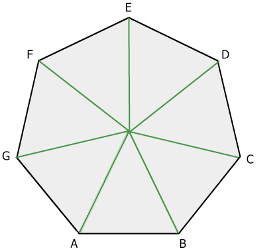
Calculations at a regular heptagon, a polygon with 7 vertices. Sometimes the term septagon is used.
Enter one value and choose the number of decimal places. Then click Calculate.

Formulas:

d = a / (2 \cdot \sin (π / 2 / 7))

e = 2 \cdot a \cdot \cos (π / 7)

h = a / (2 \cdot \tan (π / 14 / 7))

p = 7 \cdot a

A = 7 / 4 \cdot a^{2} / \tan (π / 7)

r_{c} = a / (2 \cdot \sin (π / 7))

r_{i} = a / (2 \cdot \tan (π / 7)

Angle: 5/7*180° ≈ 128,57°
14 diagonals

π = 180 ° = 3.141592653589793...

Edge length, diagonals, height, perimeter and radius have the same unit (e.g. meter), the area has this unit squared (e.g. square meter).

Heights, bisecting lines and median lines coincide, these intersect at the centroid, which is also circumcircle and incircle center. To this point, the regular heptagon is rotationally symmetric at a rotation of 360/7° or multiples of this. Furthermore, the regular heptagon is axially symmetric to the median lines. It is not point symmetric.

perimeter p, area A

sides and angles have the same size

height

bisecting lines

short diagonals, heptagram

long diagonals, heptagram

incircle and circumcircle

This shape is rather rare, but it is occasionally found as base in architecture. Some coins are heptagonal, such as the British 20 pence and 50 pence pieces. The 20 euro cent coin has seven notches which, when connected, form a regular heptagon.

The regular heptagon cannot be constructed in the Euclidean way, so it cannot be drawn using a compass and ruler alone. However, there are construction tools which allow the angle to be divided into three parts and thus the construction of the regular heptagon. Albrecht Dürer found an approximate construction using a compass and ruler which has an error of around 0.2 percent.

There are two regular heptagrams, i.e. stars with seven points, which are formed from the seven long diagonals and the seven short diagonals of the regular heptagon. Heptagrams are also rather rare; they are mainly used for decorative purposes.

↑ up