Arkusfunktionen
Arkusfunktionen oder zyklometrische Funktionen sind die Umkehrfunktionen der trigonometrischen Funktionen in deren Monotonieintervall. Eine Umkehrfunktion bedeutet für den Funktionsgraphen, dass dieser an der Geraden y=x gespiegelt wird. Die entsprechende trigonometrische Funktion wird umgekehrt gerechnet. Das Ergebnis ist ein Winkel.

Die Funktion sin(x) im Monotonieintervall [-π/2;π/2] (blau), die Gerade y=x (schwarz) und die Arkusfunktion asin(x) in ihrem gesamten Definitionsbereich (rot).
Hier ist ein kleiner Rechner, um Arkusfunktionen auszurechnen. Einen Wert eingeben, die Winkel in Radiant werden berechnet.
Arkusfunktionen werden mit dem Vorsatz a oder arc versehen. Manchmal trifft man aber auch die Schreibweise mit -1 an, z.B.
Arkussinus und Arkuskosinus
Die Umkehrfunktionen von Sinus und Kosinus sind im Intervall [-1;1] definiert. Der Arkussinus, asin(x) bzw. arcsin(x), hat den Wertebereich [-π/2;π/2]. Der Arkuskosinus, acos(x) bzw. arccos(x), hat den Wertebereich [0;π]. Der Arkussinus ist streng monoton steigend, der Arkuskosinus ist streng monoton fallend.
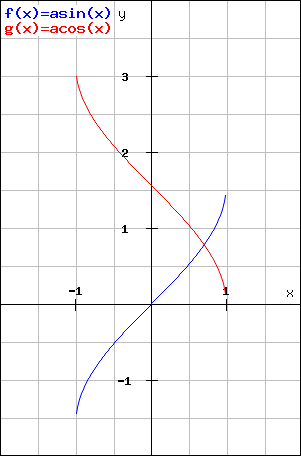
Die Graphen von Arkussinus und Arkuskosinus.
Arkustangens und Arkuskotangens
Die Umkehrfunktionen von Tangens und Kotangens sind für alle reellen Zahlen definiert. Der Arkustangens, atan(x) bzw. arctan(x), hat den Wertebereich [-π/2;π/2]. Der Arkuskotangens, acot(x) bzw. arccot(x), hat den Wertebereich [0;π]. Der Arkustangens ist streng monoton steigend, der Arkuskotangens ist streng monoton fallend.

Die Graphen von Arkustangens und Arkuskotangens.
Arkussekans und Arkuskosekans
Die Umkehrfunktionen von Sekans und Kosekans sind in den Intervallen ]-∞;-1] und [1;∞[ definiert. Der Arkussekans, asec(x) bzw. arcsec(x), hat den Wertebereich [0;π]. Der Arkuskosekans, acsc(x), arccsc (x), acosec(x) oder arccocsec(x), hat den Wertebereich [-π/2;π/2]. Der Arkussekans ist in seinen Definitionsbereichen streng monoton steigend, der Arkuskosekans streng monoton fallend.

Die Graphen von Arkussekans und Arkuskosekans.
Anwendung
Arkusfunktionen werden da verwendet, wo trigonometrische Funktionen zurückgerechnet werden, um Winkel zu erhalten. Beispiele für den Arkussinus sind der Öffnungswinkel eines Kegels, für den Arkuskosinus der Neigungswinkel einer Treppe. Für den Arkustangens ist ein Beispiel der Bildwinkel eines Objektivs, für den Arkuskotangens der Sonnenstand bei einer bestimmten Schattenlänge.
Weiter
Oft müssen trigonometrische Funktionen quadriert werden, es gibt eigene Schreibweisen für die trigonometrischen Quadratfunktionen.
Die Graphen wurden mit dem Zeichenprogramm für Funktionsgraphen erstellt.