Trigonometrische Quadratfunktionen
Diese Funktionen sind die Quadrate der jeweiligen trigonometrischen Funktionen. Ihre Frequenz ist gegenüber Sinus und Kosinus bzw. Sekans und Kosekans verdoppelt (Periode halbiert auf π), jedoch gleich wie bei Tangens und Kotangens. Die Quadrate liefern stets positive Werte oder 0. Die Schreibweise ist:
| Sinusquadrat: | sin²(α) | = [sin(α)]² | = sin(α) * sin(α) |
| Kosinusquadrat: | cos²(α) | = [cos(α)]² | = cos(α) * cos(α) |
| Tangensquadrat: | tan²(α) | = [tan(α)]² | = tan(α) * tan(α) |
| Kotangensquadrat: | cot²(α) | = [cot(α)]² | = cot(α) * cot(α) |
| Sekansquadrat: | sec²(α) | = [sec(α)]² | = sec(α) * sec(α) |
| Kosekansquadrat: | csc²(α) | = [csc(α)]² | = csc(α) * csc(α) |
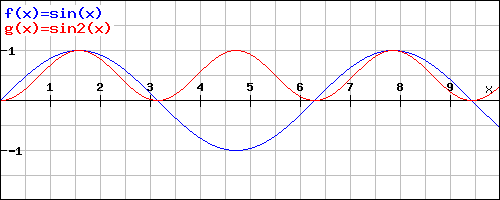
Die Funktion sin(x) (blau) und die Quadratfunktionen sin²(x) (rot) im Bereich [0;10].
Hier ist ein kleiner Rechner, um trigonometrische Quadratfunktionen auszurechnen. Einen Wert eingeben, die anderen werden berechnet.
Sinusquadrat und Kosinusquadrat
Sinusquadrat und Kosinusquadrat haben einen Wertebereich von [0;1]. Sinusquadrat hat Nullstellen und Minima bei n*π, Maxima bei (n+1/2)*π. Kosinusquadrat hat Nullstellen und Minima bei (n+1/2)*π, Maxima bei n*π. n∈ℤ. Beide sind zueinander spiegelbildlich zur Geraden y=1/2.

Die Graphen von Sinusquadrat und Kosinusquadrat.
Tangensquadrat und Kotangensquadrat
Tangensquadrat und Kotangensquadrat haben einen Wertebereich von [0;∞[. Tangensquadrat hat Nullstellen und Minima bei n*π, Polstellen bei (n+1/2)*π. Kotangensquadrat hat Nullstellen und Minima bei (n+1/2)*π, Polstellen bei n*π. n∈ℤ.

Die Graphen von Tangensquadrat und Kotangensquadrat.
Sekansquadrat und Kosekansquadrat
Sekansquadrat und Kosekansquadrat haben einen Wertebereich von [1;∞[, sie liegen um 1 höher als Tangensquadrat und Kotangensquadrat. Sekansquadrat hat Minima bei n*π, Polstellen bei (n+1/2)*π. Kosekansquadrat hat Nullstellen und Minima bei (n+1/2)*π, Polstellen bei n*π. n∈ℤ.

Die Graphen von Sekansquadrat und Kosekansquadrat.
Trigonometrischer Pythagoras
Als trigonometrischen Pythagoras bezeichnet man den Ausdruck

Trigonometrischer Pythagoras sin²(α) + cos²(α) = 1

Trigonometrischer Pythagoras 1 + tan²(α) = sec²(α)

Trigonometrischer Pythagoras 1 + cot²(α) = csc²(α)
Umkehrfunktionen
Die Umkehrfunktionen der Quadratfunktionen sind der jeweilige Arkus der Wurzel.
| Funktion | Umkehrfunktion |
|---|---|
| sin²(x) | asin(√x) |
| cos²(x) | acos(√x) |
| tan²(x) | atan(√x) |
| cot²(x) | acot(√x) |
| sec²(x) | asec(√x) |
| csc²(x) | acsc(√x) |

Die Umkehrfunktionen von Sinusquadrat und Kosinusquadrat sind im Intervall [0;1] definiert und haben einen Wertebereich von [0;π/2]. Die erste ist streng monoton steigend, die zweite ist streng monoton fallend. acos(√x) = π/2 - asin(√x)

Die Umkehrfunktionen von Tangensquadrat und Kotangensquadrat sind im Intervall [0;∞[ definiert und haben einen Wertebereich von [0;π/2]. Die erste ist streng monoton steigend, die zweite ist streng monoton fallend. acot(√x) = π/2 - atan(√x).

Die Umkehrfunktionen von Sekansquadrat und Kosekansquadrat sind im Intervall [1;∞[ definiert und haben einen Wertebereich von [0;π/2]. Die erste ist streng monoton steigend, die zweite ist streng monoton fallend. Sie liegen um 1 weiter rechts als Tangensquadrat und Kotangensquadrat. asec(√x) = atan(√x-1) und acsc(√x) = acot(√x-1).
Hier ist ein kleiner Rechner, um die Umkehrfunktionen der trigonometrischen Quadratfunktionen auszurechnen. Einen Wert eingeben, die Winkel in Radiant werden berechnet.
Anwendung
Trigonometrische Quadratfunktionen tauchen relativ häufig auf. Ein Beispiel für Sinusquadrat und Kosinusquadrat findet man in der Berechnung der Länge der Schenkel bei einem Ellipsensektor. Ein Kotangensquadrat steckt in der Schrägenhöhe einer regelmäßigen Pyramide. Ein Beispiel für den Anwendung des Sekansquadrats ist die Höhe eines Antiprismas, für das Kosekansquadrates die Höhe einer regelmäßigen Kuppel.
Siehe auch Rechner für trigonometrische Potenzen.
Weiter
Es gibt noch weitere trigonometrische Funktionen: Sinus cardinalis, tanc, Versus, Exsekans und Exkosekans.
Die Graphen wurden mit dem Zeichenprogramm für Funktionsgraphen erstellt.