Rechner für Lineare Algebra

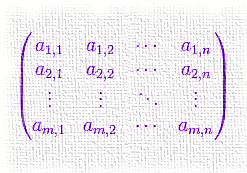
Lineare Algebra ist die Lehre von den linearen Gleichungen. Eine lineare Gleichung ist zum Beispiel 2x-3y+4z=8. Diese hat mehrere Unbekannte, x, y und z lassen sich nur eindeutig lösen, wenn man weitere unabhängige Gleichungen dieser Art hat. Lineare Gleichungen trifft man in der Mathematik oft an, zum Beispiel in der Wirtschaftsmathematik zur Beschreibung ökonomischer Zusammenhänge. Die lineare Algebra bietet komfortable Methoden zu deren Berechnung. Hier finden sich entsprechende Rechner für Matrizen, Determinanten, Gleichungssysteme und für Vektoren im ℜ³.